本日の目標

確率の基礎を復習

2.1 確率

試行(trial) : 実験や観測
(サイコロを6回ふる)
事象(event) :実験や観測の結果の集まり
(3の目が2回出る)

数学的確率

\(\frac{r}{N}\)

\(N\): ある試行で同じ程度に起こり得ると期待される全ての場合の数
\(r\): Nのうち事象\(A\)が起こる場合の数

1の目が出る数学的確率

\(p=\frac{1}{6}\)

N: \(サイコロの出目全ての場合の数=\{1,2,3,4,5,6\}= 6\)
r: \(1の目がおこる場合の数=\{1\}= 1\)

目の出方が公平に作られたサイコロを投げたとき、1の目が出る確率が\(p=\frac{1}{6}\)であるが、現実では、そのようなサイコロは存在しない

統計的確率

\(\frac{r}{n}\)を数学的確率\(p\)の近似と考える。

\(n\): 試行数(サイコロを投げた回数)
\(r\): 事象(1の目)が出た回数

2.2 現代的確率

2.2.1 事象

事象: ある試行の結果の集まり
全事象(標本空間): 試行によって起こりうるすべての結果
部分集合: 全事象のうちの特定の事象

さいころを投げて、出る目を全て観察した場合の全事象
\(U=\{1, 2, 3, 4, 5, 6\}\)

偶数が出る目の事象\(A=\{2, 4, 6\}\)

事象\(A\)は全事象\(U\)の部分集合

確率	表記	意味
全事象	\(U\)	標本空間
和事象	\(A\cup B\)	2つの事象A Bの少なくとも一方が起こる確率
積事象	\(A\cap B\)	2つの事象A, Bが同時に起こる確率
空事象	\(\phi\)	どんな結果も含んでいないという事象
排反事象	\(A\cap B=\phi\)	2つの事象A,Bが決して同時には起こらないという事象
余事象	\(A^c\)	事象Aが起こらないという事象

\(A_1, A_2, \dots, A_n\)の和事象

\[\displaystyle A_1\cup A_2 \cup \dots \cup A_n = \bigcup_{i=1}^n A_i \]

\(A_1, A_2, \dots, A_n\)の積事象

\[\displaystyle A_1\cap A_2 \cap \dots \cap A_n = \bigcap_{i=1}^n A_i \]

ベン図による理解

排反事象 \(A\cap B=\phi\)
(事象AとBは独立: Aの発生確率はBの発生確率に影響を与えない)

require(venneuler)
v <- venneuler(c(A = 450, B = 450, `A&B` = -5))
v$colors <- c(0.66, 0.66)
plot(v)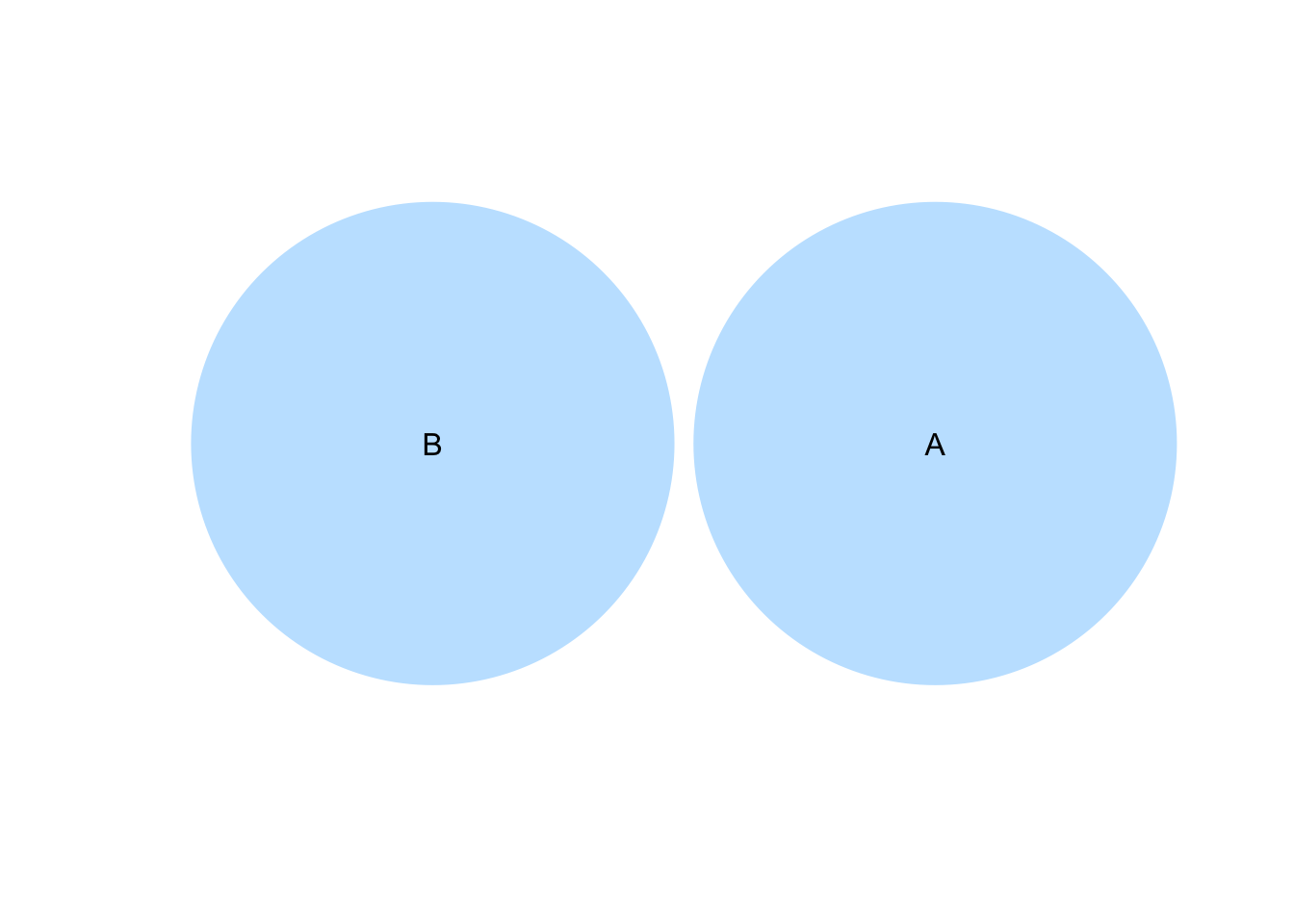

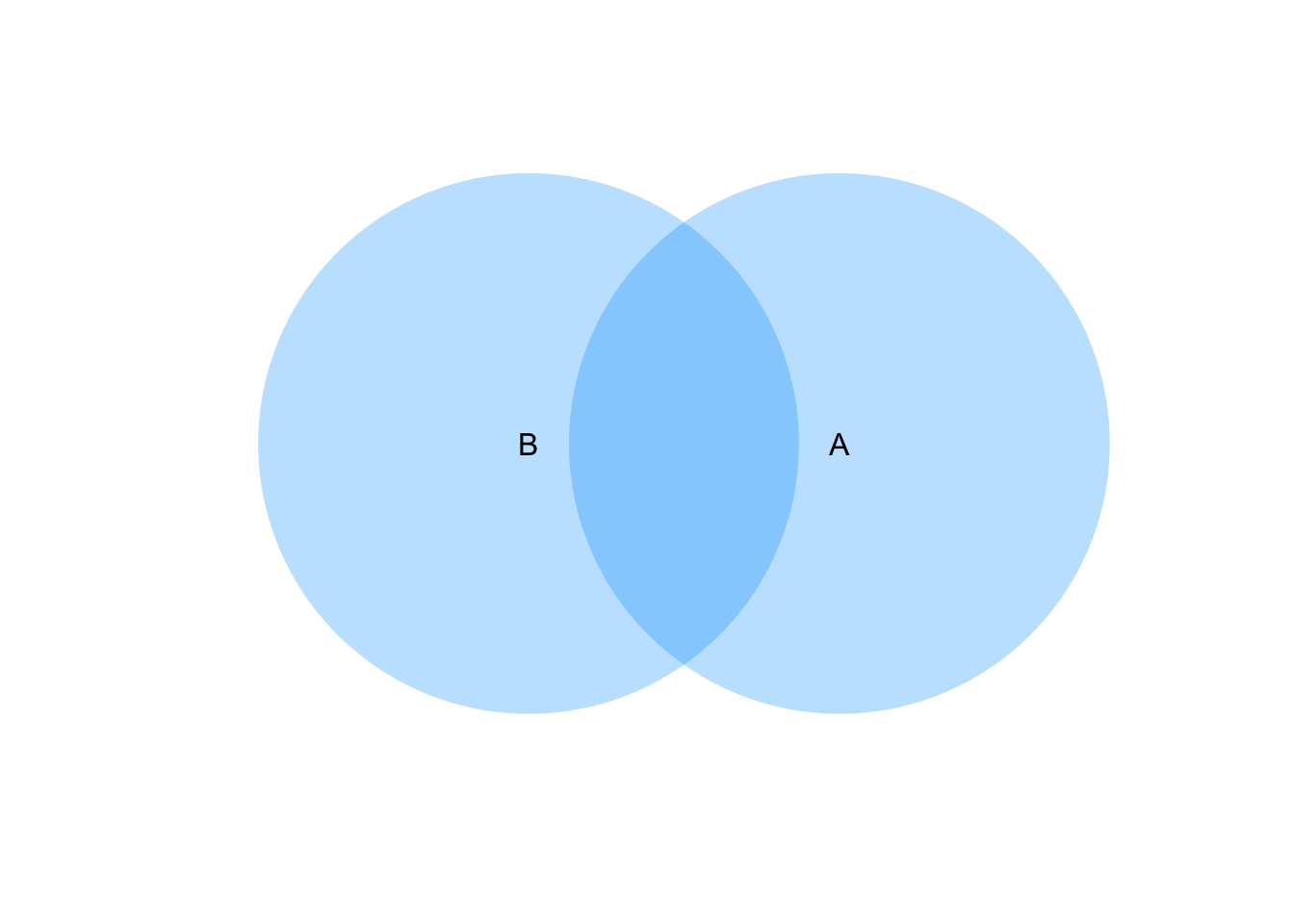
和事象 (事象Aと事象Bの合計: 重複部の扱いは後ほど)

\[\displaystyle A_1\cup A_2 \cup \dots \cup A_n = \bigcup_{i=1}^n A_i \]

積事象 (重複部のみ)

\[\displaystyle A_1\cap A_2 \cap \dots \cap A_n = \bigcap_{i=1}^n A_i \]

v <- venneuler(c(A = 450, B = 450, `A&B` = 200))
v$colors <- c(0.66, 0.66)
plot(v)

2.2.2 確率

確率の定義

標本空間\(U\)の部分集合\(A\)に対して、P{A}が以下の性質が満たす場合、P{A}を\(A\)の確率と呼ぶ

\(P\{A\}\geqq 0\)
\(P\{U\}= 1\)
\(n\)個の事象\(A_1, A_2, \dots, A_n\)が互いに排反の時
\(A_1\cup A_2 \cup \dots \cup A_n = P\{A_1\}+P\{A_2\}+,\dots,+P\{A_n\}\)
を満たし、\(P\{A\}\)にたいして正の実数が一意に対応されている

余事象の法則

\(P\{A^c\}=1-P\{A\}\): 余事象の確率は、1からAの確率引く

和事象の法則

事象\(A\)と事象\(B\)が排反: \(P\{A \cup B\}=P\{A\}+P\{B\}\)

事象\(A\)と事象\(B\)が排反でない
\(P\{A \cup B\}=P\{A\}+P\{B\}-P\{A \cap B\}\) 重なってる分(積事象)を引く

事象の独立

条件付き確率 (事象AとBが独立ではない場合の確率)

事象Aが起こったという条件のもとで事象Bが起こる確率
\(P\{B|A\}=\frac{P\{A \cap B\}}{P\{A\}}\)
ただし、\(P\{A\}\neq 0\)

事象\(A\)と事象\(B\)が独立な場合

\(P\{B|A\}=P\{B\}\)
独立でない場合は従属であるという。

事象Aと事象Bが独立であるとき
(\(P\{B|A\}\)を条件付き確率の\(P\{B\}\)に代入すると)
\[ \displaystyle P\{A \cap B\}=P\{A\} \cdot P\{B\} \]

積事象の法則

\[ \displaystyle P\{A \cap B\}=P\{A\}\dot P\{B\} (AとBが独立) \]

\[ \displaystyle P\{A \cap B\}=P\{A\}\dot P\{B|A\} (P\{A\}\neq0のとき) \]

\[ \displaystyle P\{A \cap B\}=P\{A\}\dot P\{A|B\} (P\{B\}\neq0のとき) \]