本日の目標

回帰係数の算出方法を理解する

データに対して回帰直線を当てはめる

1.4 回帰直線

散布図をみると、直線的な傾向が見て取れる2つの変数(X, Y)があるとする

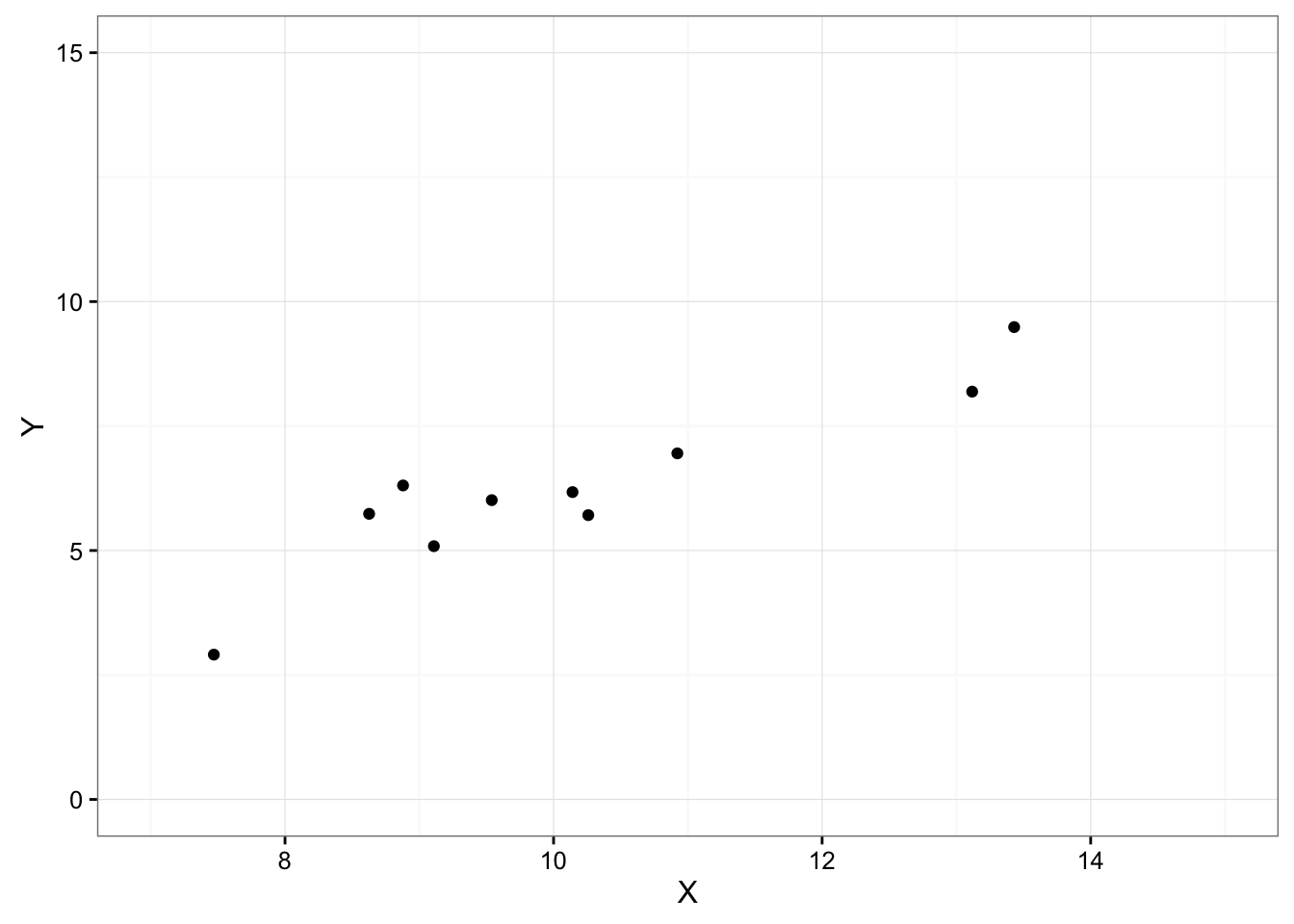
例えば、Xが勉強時間、Yがテストの得点として、テストの得点を勉強時間で説明・予測したいとする。
(勉強時間(X)が(何点)増えるとテストの得点が(何点)上がるか?が知りたい)

結果変数(目的変数): 説明・予測される変数(Y)
原因変数(説明変数): 説明・予測する変数(X)

回帰直線

テストの得点(Y)を勉強時間(X)で説明するにあたって、ここでは、一次関数$\displaystyle y=a+bx$を利用する
$\displaystyle テストの得点(y)=a+b\times 勉強時間(x)$

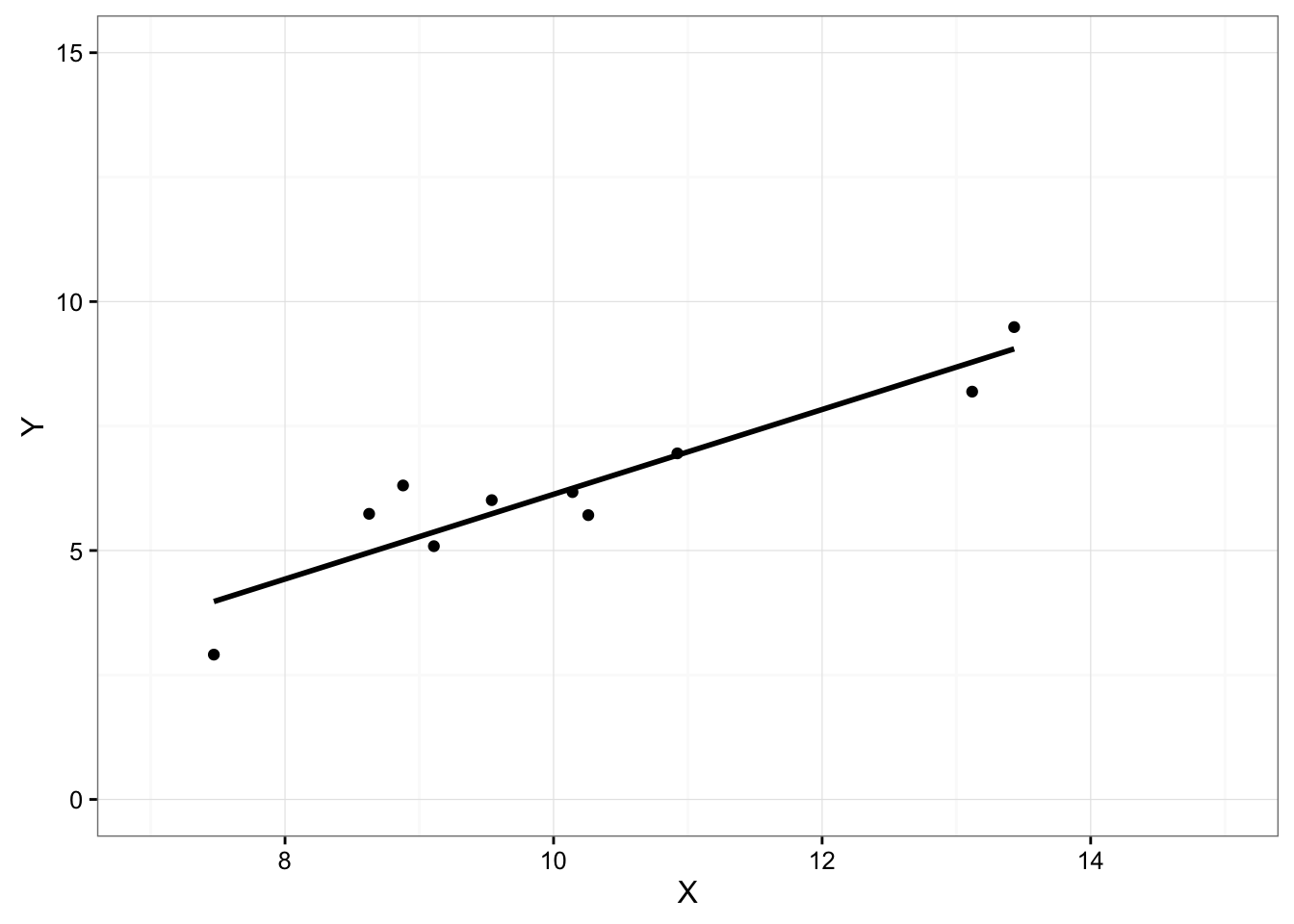
回帰直線: この一次関数から得られる直線
切片(a): 説明変数が最小の場合のYの値
傾き(b): 回帰直線の傾き

切片(a)と傾き(b)の値を動かすことで、異なる線が描かれる。
YをXが説明する直線を引きたい。
どのような基準でaとbを求めるか?

最小二乗法

モデルから予測された値(回帰直線)と実データ間の乖離(残差)が最小になるよう(最小二乗基準)に、切片(a)と傾き(b)を推定する

$\displaystyle D=\sum_{i=1}^n\varepsilon_i^2=\sum_{i=i}^2\{y_i-(a+bx_i)\}^2$

残差: $\varepsilon_i(i=1,\dots, n)$

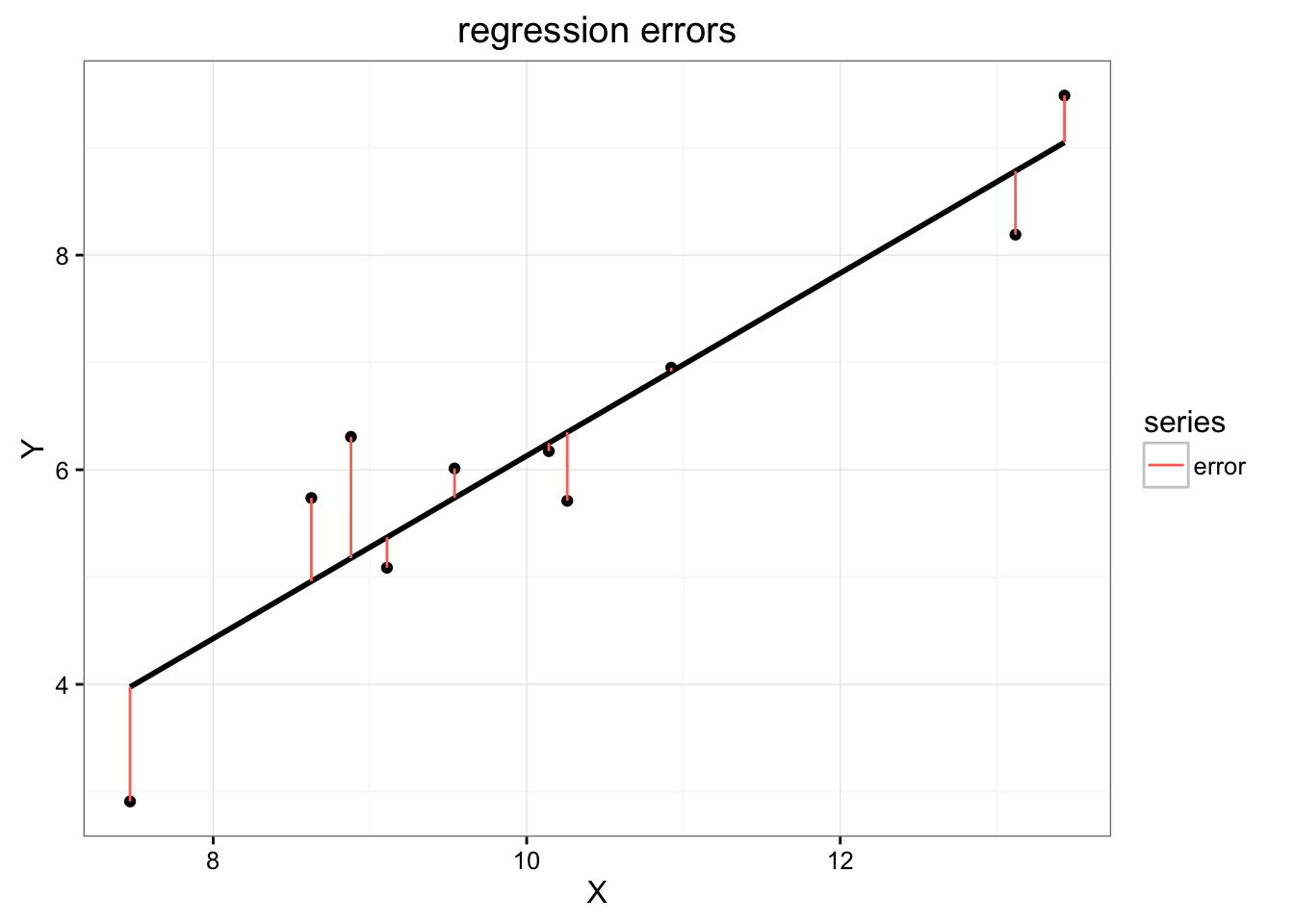
図の赤線が残差
残差の二乗和が最小二乗基準(D)

切片と回帰係数の導出

最小二乗基準を、切片(a)と回帰係数(b)について偏微分し導出される方程式を整理していくことで、最終的に、以下のように、簡単に算出される。

$\displaystyle 回帰係数(傾き:b)=\frac{XとYの共分散}{Xの分散}$

$\displaystyle 切片(a)=Yの平均-回帰係数(b)\times Xの平均$

導出過程

$D$(最小二乗基準)を、切片(a)と傾き(b)について偏微分し、ともに0とする

\[ \left\{ \begin{eqnarray} \displaystyle \frac{\partial D}{\partial a}=-2\sum_{i=i}^n\{y_i-(a+bx_i)\}&=&0\tag{2.1} \\ \displaystyle \frac{\partial D}{\partial a}=-2\sum_{i=i}^n\{y_i-(a+bx_i)\}&=&0\tag{2.2} \end{eqnarray} \right. \]

これにより、次の方程式が得られる。

\[\left\{ \begin{eqnarray} \displaystyle \sum_{i=1}^n{y_i}&=&na+b\sum_{i=i}^n x_i\tag{1} \\ \displaystyle \sum_{i=1}^n{x_i}{y_i}&=&a\sum_{i=i}^n x_i+b\sum_{i=i}^1 x_i^2\tag{2} \end{eqnarray} \right. \]

これにより回帰係数(b)が以下で求められる

\[ \begin{eqnarray} \displaystyle b&=&\frac{n\sum_{i=1}^n x_i y_i-\sum_{i=1}^n x_i \sum_{i=1}^n y_i}{n\sum_{i=1}^n {x_i}^2-(\sum_{i=1}^n {x_i}^2)} \\ \displaystyle &=&\frac{n\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{n\sum_{i=1}^n( x_i-\bar x)} \\ \displaystyle &=&\frac{S_{xy}}{S_x^2} \end{eqnarray} \]

2.2式の両辺を$n$で割ると$\bar{y}=a+b\bar{x}$となり $y-\bar{y}=b(x-\bar{x})$ が得られる

よって、以下で切片(b)が求められる

$a=\bar{y}-b\bar{x}$

以下の表のように、必要になる値をまとめると、回帰係数(b)は$A/B$で簡単に求められる

ペア番号	$x_i$	$y_i$	$(x_i-\bar{x})(y_i-\bar{y})$	$n( x_i-\bar x)$
1	$x_1$	$y_1$	$(x_1-\bar{x})(y_1-\bar{y})$	$n( x_1-\bar x)$
2	$x_2$	$y_2$	$(x_2-\bar{x})(y_2-\bar{y})$	$n( x_2-\bar x)$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
5	$x_n$	$y_n$	$(x_n-\bar{x})(y_n-\bar{y})$	$n( x_n-\bar x)$
合計	$S_x$	$S_y$	$A$	$B$
平均	{x}	{y}

演習問題

1.1

(問) 4,8,10,12,16の平均$\bar{x}$,分散$S^2$, 標準偏差$s$を求めよ (答) 平均$\bar{x}=10$,分散$S^2=16$, 標準偏差$s=4$を求めよ

平均 \[ \begin{eqnarray} \displaystyle \bar{x} &=& \frac{1}{n}n\sum_{i=1}^n x_i \\ \displaystyle &=&\frac{4+8+10+12+16}{5} \\ \displaystyle &=&\frac{50}{5} \\ &=&10 \end{eqnarray} \]
分散 \[ \begin{eqnarray} \displaystyle \S^2 &=& \frac{1}{n}n\sum_{i=1}^n (x_i-\bar{x})^2 \\ \displaystyle &=&\frac{(4-10)^2+(8-10)^2+(10-10)^2+(12-10)^2+(16-10)^2}{5} \\ \displaystyle &=&\frac{80}{5} \\ &=&16 \end{eqnarray} \]
標準偏差 \[ \begin{eqnarray} \displaystyle \S &=& \sqrt{S^2} \\ \displaystyle &=&\sqrt{16} \\ \displaystyle &=&4 \\ &=&16 \end{eqnarray} \]

1.2

(問) A, B2クラスのそれぞれ40名の数学の得点を調べ、次の度数分布表を作成した。各クラスの平均,分散, 標準偏差を求めよ。

(答) A, B2クラスのそれぞれ40名の数学の得点を調べ、次の度数分布表を作成した。各クラスの平均,分散, 標準偏差を求めよ。

クラスA

平均 \[ \begin{eqnarray} \displaystyle \bar{x} &=& \frac{1}{n}n\sum_{i=1}^n x_i^*f_i \\ \displaystyle &=&\frac{35\times 1+45\times 4+55\times 6+65\times 18+75\times 7+85\times 3+95\times 1}{40} \\ \displaystyle &=&\frac{2590}{40} \\ &=&64.75 \end{eqnarray} \]
分散 \[ \begin{eqnarray} \displaystyle s^2 &=& \frac{1}{n}n\sum_{i=1}^n (x_i^*-\bar{x})^2 \\ \displaystyle &=&\frac{(35-64.75)^2\times 1+(45-64.75)^2\times 4+(55--64.75)^2\times 6+(65--64.75)^2\times 18+(75--64.75)^2\times 7+(85--64.75)^2\times 3+(95\times 1}{40} \\ \displaystyle &=&\frac{5897.5}{40} \\ &=&147.438 \end{eqnarray} \]
標準偏差 \[ \begin{eqnarray} \displaystyle s &=& \sqrt{s^2} \\ \displaystyle &=&\sqrt{147.438} \\ \displaystyle &=&12.142 \end{eqnarray} \]

クラスB

平均 \[ \begin{eqnarray} \displaystyle \bar{y} &=& \frac{1}{n}n\sum_{i=1}^n y_i^*f_i \\ \displaystyle &=&\frac{35\times 0+45\times 1+55\times 7+65\times 25+75\times 5+85\times 2+95\times 0}{40} \\ \displaystyle &=&\frac{2600}{40} \\ &=&65 \end{eqnarray} \]
分散 \[ \begin{eqnarray} \displaystyle s^2 &=& \frac{1}{n}n\sum_{i=1}^n (y_i^*-\bar{y})^2 \\ \displaystyle &=&\frac{(35-64.75)^2\times 0+(45-64.75)^2\times 1+(55--64.75)^2\times 7+(65-64.75)^2\times 25+(75-64.75)^2\times 5+(85-64.75)^2\times 2+(95\times 0}{40} \\ \displaystyle &=&\frac{2400}{40} \\ &=&60 \end{eqnarray} \]
標準偏差 \[ \begin{eqnarray} \displaystyle s &=& \sqrt{s^2} \\ \displaystyle &=&\sqrt{60} \\ \displaystyle &=&7.746 \end{eqnarray} \]

1.3

2変量$(x,y)$を測定し、以下の結果を得た。平均、分散、標準偏差を求め、共分散、相関を求めよ。

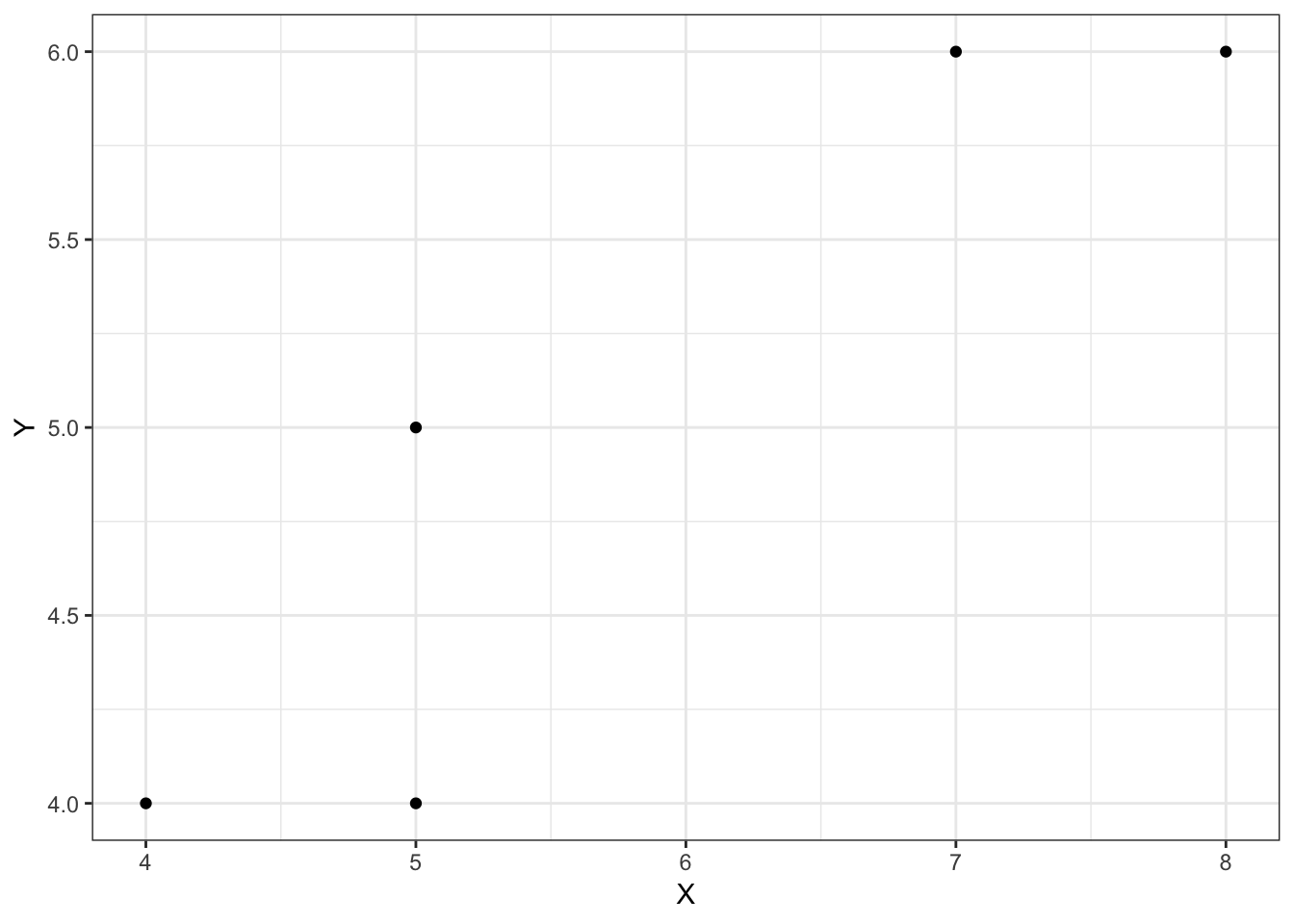
相関係数 \[ \begin{align} r=\frac{S_{xy}}{S_xS_y} \end{align} \]

共分散 \[ \begin{align} S_{xy}=\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y}) \end{align} \]

1.4

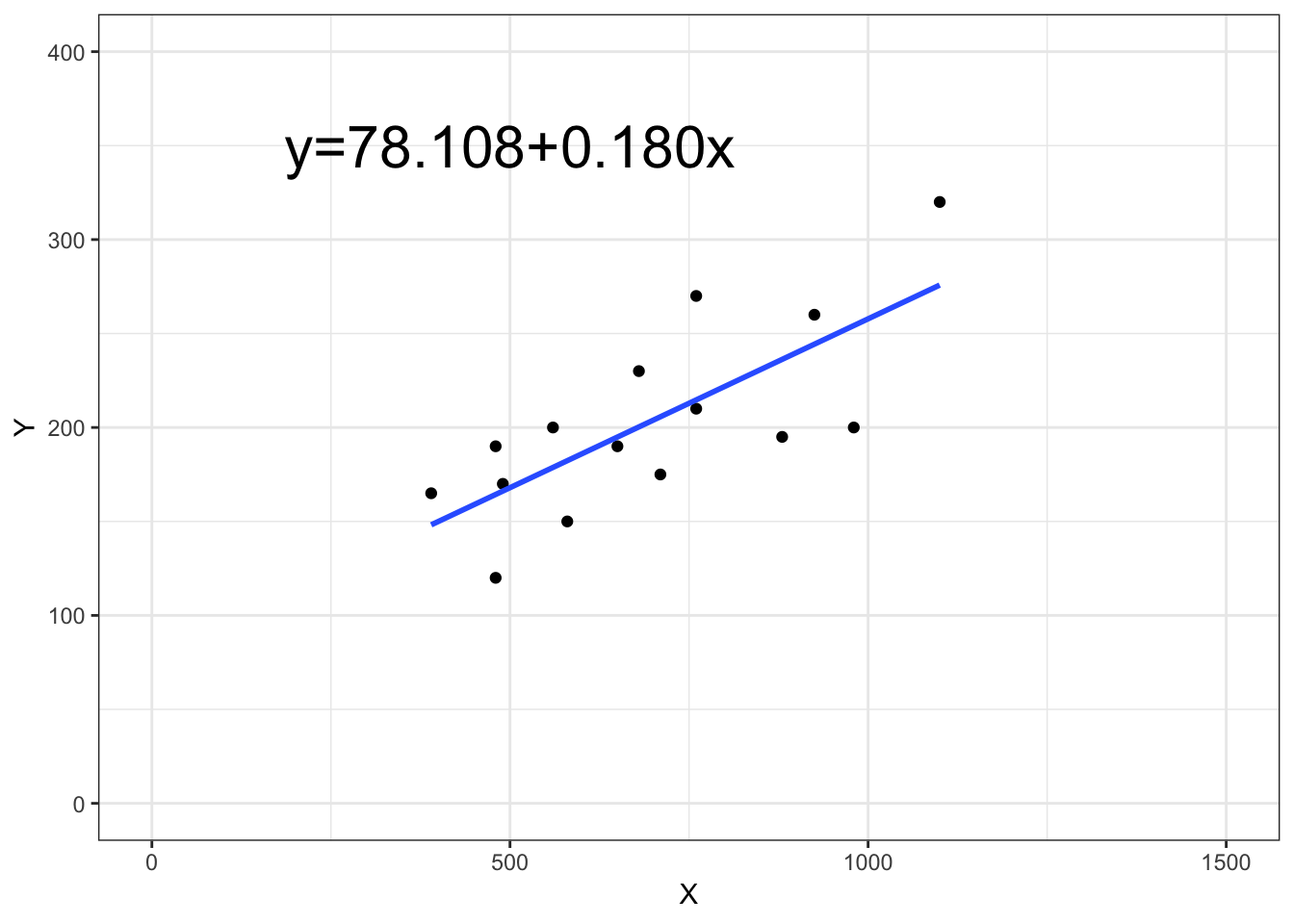
社会人15人の1年間の実収入と食費支出の関係を調べ以下のデータを得た。この表をもとに回帰係数を算出し、回帰直線を図示せよ。

1.4

社会人15人の1年間の実収入と食費支出の関係を調べ以下のデータを得た。この表をもとに回帰係数を算出し、回帰直線を図示せよ。

\[ \begin{eqnarray} \displaystyle 回帰係数(傾き:b)&=&\frac{XとYの共分散}{Xの分散} \\ \displaystyle &=&\frac{108225}{602250} \\ \displaystyle &=&0.180 \end{eqnarray} \]

\[ \begin{eqnarray} \displaystyle 切片(a)&=&Yの平均-回帰係数(b)\times Xの平均$ \\ \displaystyle &=&203-0.18\times 695$ \\ \displaystyle &=&78.103$ \end{eqnarray} \]

回帰直線: $y=78.108+0.180x$

ペア番号	\(x_i\)	\(y_i\)	\((x_i-\bar{x})(y_i-\bar{y})\)	\(n( x_i-\bar x)\)
1	\(x_1\)	\(y_1\)	\((x_1-\bar{x})(y_1-\bar{y})\)	\(n( x_1-\bar x)\)
2	\(x_2\)	\(y_2\)	\((x_2-\bar{x})(y_2-\bar{y})\)	\(n( x_2-\bar x)\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)
5	\(x_n\)	\(y_n\)	\((x_n-\bar{x})(y_n-\bar{y})\)	\(n( x_n-\bar x)\)
合計	\(S_x\)	\(S_y\)	\(A\)	\(B\)
平均	{x}	{y}