統計資料 (statistical data, データ)

調査、実験、既存の資料を調べて得られたデータ

例) ある小学校1年生の身長, 体重, 性別, 学校での満足度を知りたい

集団と個体

• 調査対象となる集団 = 小学校
  
• 集団を構成する個体 = 児童

変量と属性

変量(variate) : 個体ごとに変動する数量的な特性
例) 身長, 体重
(Aさんは150cm, Bさんは160cm, Cさんは155cm…)
(Aさんは50kg, Bさんは60kg, Cさんは55kg…)

属性 (attribute): 個体ごとに変動する質的な特性
例) 性別 (男, 女), 学校での満足度(満足, 不満足)
(Aさんは男, Bさんは女, Cさんは男…)
(Aさんは満足, Bさんは満足, Cさんは不満…)

###　

###　

###　

変数の種類

連続変量: 測定値が実数値で表される
- 目盛りに句切れがなく連続している (小数点がつく)
- 例)　身長, 体重

離散変数: 測定値が整数でしか表せない
- 目盛りに句切れがある　(小数点がつかない)
- 例) 満足度(満足してない=o, 満足している=1)

###　

得られた資料の整理手順

1. 統計資料の入手
2. 度数分布表の作成
3. ヒストグラムを作成し, 視覚的に資料の分布を把握
4. 代表値, 散布度等の特性値を求め、資料の分布の特徴を数量的に把握

1. 最小値と最大値をみつける。

　最小値を \(\alpha_0\) 、最大値を \(\alpha_n\) とする

# 最大値と最小値をみつける
Xmax <- max(X)
Xmin <- min(X)

最大値\(X_{max}\)は60, 最小値\(X_{min}\)は21

2. 級の数\(k\)を決める

• 最大値から最小値を引き, \(k\)等分し、分点を, \(\alpha_1,\alpha_2,\dots,\alpha_{k-1}\)とする。

  \(k\)を4とすると…

# (最大値 - 最小値) / 級の数
k = 4

# 20~60を10ごと区切ると4等分になる
(Xmax - (Xmin - 1))/k

[1] 10

　先の例の分点は, 以下のようになる。
　- \(\alpha_1 = 30\)
　- \(\alpha_2 = 40\)
　- \(\alpha_3 = 50\)

級の数(\(k\))が大きすぎると分布の特性が表しにくく、小さすぎると部分的な特性が消されるが、データの大きさ(個数)\(n\)に関連して定める。

3. 級限界を決める。

• 級： \[ \begin{align} \alpha_0\sim\alpha_1,\alpha_1\sim\alpha_2,\dots, \alpha_{k-1}\sim\alpha_k(\alpha_k=\alpha_n) \end{align} \]

• 第1の級: \(\alpha_0\sim\alpha_1\)
  • 第1の級の級下限界\(\alpha_0\)
  • 第1の級の級上限界\(\alpha_1\)
  • これらを単に級限界と呼ぶ。

4. 級代表値を求める。

第\(i\)の級の代表値： \[ \begin{align} x^*_i=\frac{\alpha_i+\alpha_{i-1}}{2} (i=1,\dots,k) \end{align} \]

5. 各級の度数と合計を求める.

度数= 各級に属するデータの数\(f_i(i=1,\dots,k)\)
度数の合計 = \(n(n=f_1+f_2+\dots+f_k)\)

度数分布を図示し視覚的に理解する

1. 度数分布表を作成 (級ごとの度数を求める)
2. 得点を横軸、度数を縦軸にとる
3. 各階級の度数をプロットする

# 100人の得点をenglishに格納
english <- c(20, 29, 83, 50, 33, 44, 41, 60, 66, 74, 38, 83, 46, 33, 77, 57, 
    50, 77, 73, 61, 41, 15, 39, 45, 56, 67, 63, 86, 84, 84, 54, 50, 59, 58, 
    63, 70, 78, 50, 64, 59, 63, 75, 63, 60, 76, 89, 85, 62, 68, 75, 77, 68, 
    78, 79, 87, 65, 63, 77, 72, 61, 87, 30, 24, 80, 67, 61, 70, 30, 71, 64, 
    99, 94, 37, 31, 37, 71, 71, 69, 63, 56, 17, 41, 46, 47, 76, 61, 87, 51, 
    73, 69, 34, 31, 53, 24, 50, 77, 68, 62, 56, 76)

# 小さい順に並び替えると
sort(english)

 [1] 15 17 20 24 24 29 30 30 31 31 33 33 34 37 37 38 39 41 41 41 44 45 46
[24] 46 47 50 50 50 50 50 51 53 54 56 56 56 57 58 59 59 60 60 61 61 61 61
[47] 62 62 63 63 63 63 63 63 64 64 65 66 67 67 68 68 68 69 69 70 70 71 71
[70] 71 72 73 73 74 75
 [ reached getOption("max.print") -- omitted 25 entries ]

度数分布表を作成

• 今回は, 教科書に合わせて, 最小値を9.5, 最大値を99.5とし, 級数を9とする。
• 今回は, 10ごとの分点となり, 各級の級代表値は級の区間の中点になる。
• 各級の度数をカウントする

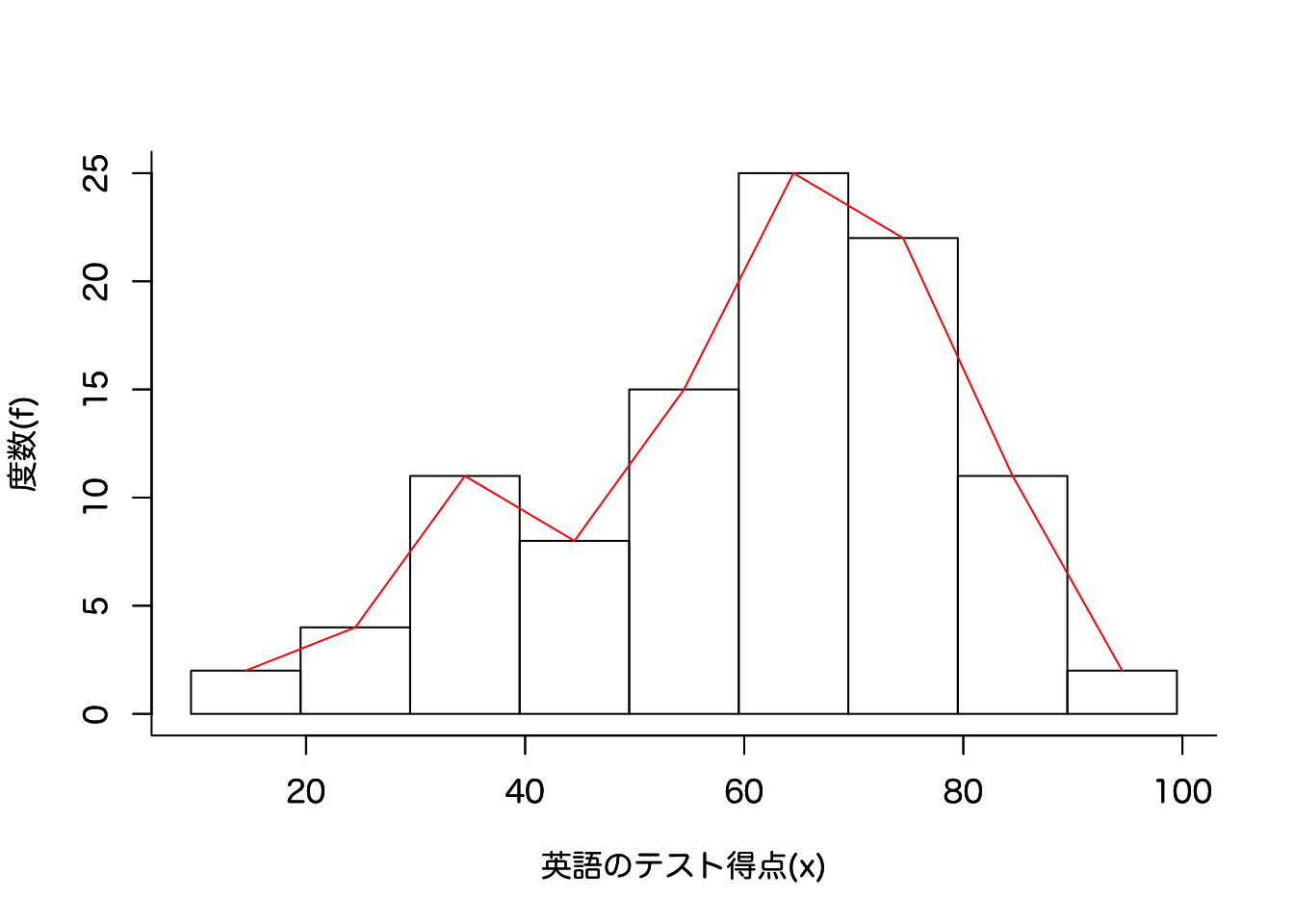
ヒストグラムをプロット

• 赤線は度数折線 (各級の代表値を直線結んだ線)
• 柱状グラフはヒストグラム (各級の度数を柱状グラフで表現)

# 最大値を99.5, 最小値を9.5とし、9階級で整理する
h1 <- hist(english, breaks = seq(9.5, 99.5, 10), plot = F)

# 級の数
k <- length(h1$counts)

class_names <- NULL  # 級の名前格納用
rep_k <- NULL  # 級の代表値格納用
for (i in 1:k) {
    class_names[i] <- paste(h1$breaks[i], "～", h1$breaks[i + 1])
    rep_k[i] <- (h1$breaks[i + 1] + h1$breaks[i])/2
}

frequency_table <- data.frame(級 = class_names, 級代表値 = rep_k, 度数 = h1$counts)
frequency_table

            級 級代表値 度数
1  9.5 ～ 19.5     14.5    2
2 19.5 ～ 29.5     24.5    4
3 29.5 ～ 39.5     34.5   11
4 39.5 ～ 49.5     44.5    8
5 49.5 ～ 59.5     54.5   15
6 59.5 ～ 69.5     64.5   25
7 69.5 ～ 79.5     74.5   22
8 79.5 ～ 89.5     84.5   11
9 89.5 ～ 99.5     94.5    2

# 級1の度数
length(english[english <= 19.5])

[1] 2

# 級2の度数
length(english[english >= 19.5 & english <= 29.5])

[1] 4

# 級3の度数
length(english[english >= 29.5 & english <= 39.5])

[1] 11

# 級4の度数
length(english[english >= 39.5 & english <= 49.5])

[1] 8

# 級5の度数
length(english[english >= 49.5 & english <= 59.5])

[1] 15

# 級6の度数
length(english[english >= 59.5 & english <= 69.5])

[1] 25

# 級7の度数
length(english[english >= 69.5 & english <= 79.5])

[1] 22

# 級8の度数
length(english[english >= 79.5 & english <= 89.5])

[1] 11

# 級9の度数
length(english[english >= 89.5 & english <= 99.5])

[1] 2

平均値

• データが\(x_1,x_2,\dots,x_n\)の時の平均値:

\[ \begin{align} \bar{x}=\frac{x_1+x_2+\dots+x_n}{n}=\frac{1}{n}\sum_{i=1}^n x_i \end{align} \]

• \(k\)個の級に分けて、その級代表値を\(x^*_1,x^*_2,\dots,x^*_k\)の時の平均値:

\[ \begin{align} \bar{x}=\frac{x^*_1 f_1+x^*_2 f_2+\dots+x^*_k f_k}{n}=\frac{1}{n}\sum_{i=1}^k x^*_i f_i \end{align} \]

• 加重平均:
  \(x_1\)が\(f_1\)個,\(x_2\)が\(f_2\)個,\(\dots\),\(x_k\)が\(f_k\)個あるときに上式を用いて算出する平均値

###　

中央値

• データ\(x_1,x_2,\dots,x_n\)を小さい順に並べたものを以下で表す。 \[ \begin{align} x^{(1)}≦x^{(2)}≦\dots≦x^{(n-1)}≦x^{(n)} \end{align} \]

• この時、中央の値を中央値(median)といい\(\tilde{x}\)で表す。

  \(n\)が奇数の時の中央値 \[ \begin{align} \tilde{x}=x^{((n+1)/2)} \end{align} \]

  \(n\)が偶数の時の中央値 \[ \begin{align} \tilde{x}=\frac{1}{2}(x^{(n/2)}+x^{(n/2+1)}) \end{align} \]

分散

\[ \begin{align} s^2=\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\dots+(x_n-\bar{x})^2}{n}=\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2 \end{align} \]

\(s^2\)が小さとき、データは\(\bar{x}\)付近に密集し、バラツキが大きいと\(s^2\)はでかくなる。

左図: 平均=15, 分散=1, 右図: 平均=15, 分散=5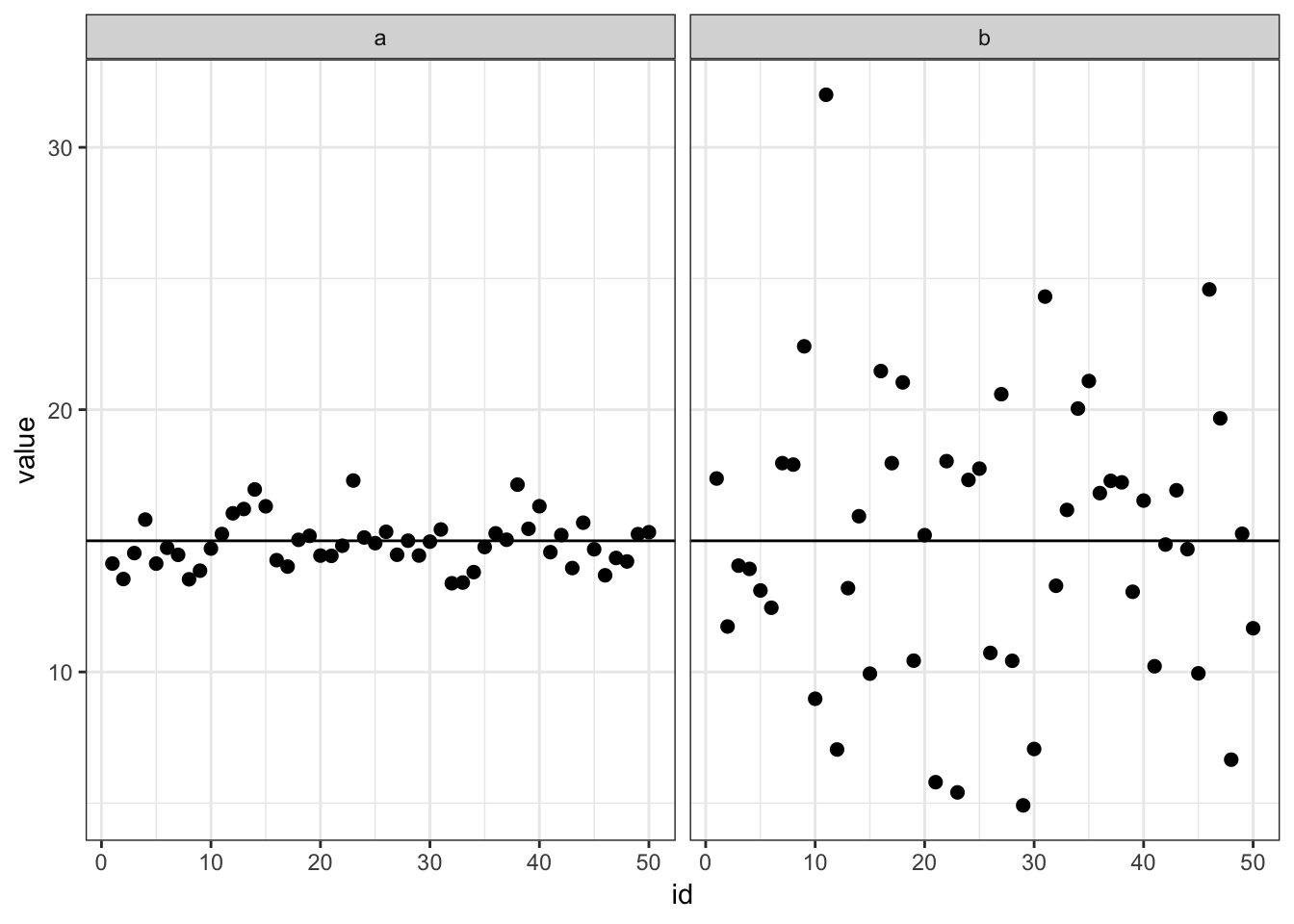 

標準偏差

• 分散の平方根

\[ \begin{align} s^2=\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\dots+(x_n-\bar{x})^2}{n}=\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2 \end{align} \]

\[ \begin{align} s^2=\frac{1}{n}\sum_{i=1}^n (x^2_i)-(\bar{x})^2 \end{align} \]

\[ \begin{align} s=\sqrt{s^2} \end{align} \]

• 級に分けられたデータ
  \[ \begin{align} s^2=\frac{1}{n}\sum_{i=1}^n (x^*_i-\bar{x})^2 f_i=\frac{1}{n}\sum_{i=1}^n (x^*_i)^2 f_i-(\bar{x})^2 \end{align} \]

\[ \begin{align} s=\sqrt{s^2} \end{align} \]

\[ \begin{align} n=f_1+f_2+\dots+f_k \end{align} \]

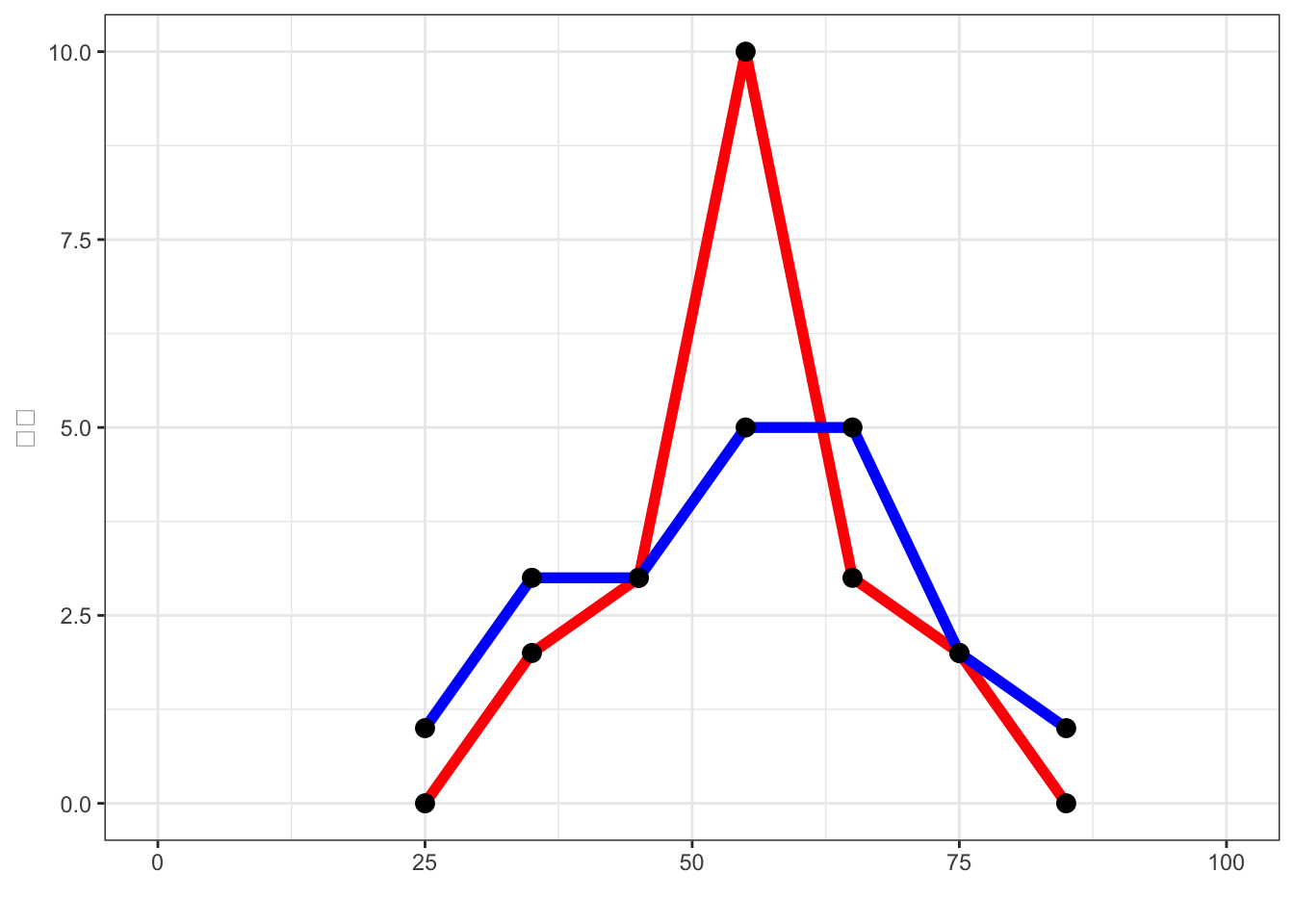
度数折れ線

• 赤がクラスA, 青がクラスB

平均: 級代表値を使用

\[ \begin{align} \bar{x}=\frac{x^*_1 f_1+x^*_2 f_2+\dots+x^*_k f_k}{n}=\frac{1}{n}\sum_{i=1}^k x^*_i f_i \end{align} \]

• クラスAの平均

\[ \begin{align} \bar{x}=\frac{25\times 0+35\times 2+45\times 3+55\times 10+65\times 3+75\times 2+85\times 0}{20} = 55 \end{align} \]

# 手計算
((25 * 0) + (35 * 2) + (45 * 3) + (55 * 10) + (65 * 3) + (75 * 2) + (85 * 0))/20

[1] 55

# 合計を算出するsum関数を使う
代表値 <- c(25, 35, 45, 55, 65, 75, 85)
Aクラスの度数 <- c(0, 2, 3, 10, 3, 2, 0)
Aクラスの人数 <- 20
sum(代表値 * Aクラスの度数)/Aクラスの人数

[1] 55

• クラスBの平均

\[ \begin{align} \bar{x}=\frac{25\times 1+35\times 3+45\times 3+55\times 5+65\times 5+75\times 2+85\times 1}{20} = 55 \end{align} \]

# 手計算
((25 * 1) + (35 * 3) + (45 * 3) + (55 * 5) + (65 * 5) + (75 * 2) + (85 * 1))/20

[1] 55

# 合計を算出するsum関数を使う
代表値 <- c(25, 35, 45, 55, 65, 75, 85)
Bクラスの度数 <- c(1, 3, 3, 5, 5, 2, 1)
Bクラスの人数 <- 20
sum(代表値 * Bクラスの度数)/Bクラスの人数

[1] 55

分散: 級代表値を使用

\[ \begin{align} s^2=\frac{1}{n}\sum_{i=1}^n (x^*_i-\bar{x})^2 f_i=\frac{1}{n}\sum_{i=1}^n (x^*_i)^2 f_i-(\bar{x})^2 \end{align} \]

• 標準偏差

\[ \begin{align} s=\sqrt{s^2} \end{align} \]

• クラスAの分散

\[ \begin{align} s^2=\frac{(25-55)^2\times 0+(35-55)^2\times 2+(45-55)^2\times 3+(55-55)^2\times 10+(65-55)^2\times 3+(75-55)^2\times 2+(85-55)^2\times 0}{20}= 110 \end{align} \]

# 手計算
(((25 - 55)^2) * 0 + ((35 - 55)^2) * 2 + ((45 - 55)^2) * 3 + ((55 - 55)^2) * 
    10 + ((65 - 55)^2) * 3 + ((75 - 55)^2) * 2 + ((85 - 55)^2) * 0)/20

[1] 110

# 合計を算出するsum関数を使う
代表値 <- c(25, 35, 45, 55, 65, 75, 85)
Aクラスの度数 <- c(0, 2, 3, 10, 3, 2, 0)
Aクラスの人数 <- 20
Aクラスの平均 <- 55

sum(((代表値 - Aクラスの平均)^2) * Aクラスの度数)/Aクラスの人数

[1] 110

• クラスAの標準偏差

\[ \begin{align} s=\sqrt{110}\risingdotseq 10.488 \end{align} \]

print(sqrt(110), digits = 5)

[1] 10.488

• クラスBの分散

\[ \begin{align} s^2=\frac{(25-55)^2\times 1+(35-55)^2\times 3+(45-55)^2\times 3+(55-55)^2\times 5+(65-55)^2\times 5+(75-55)^2\times 2+(85-55)^2\times 1}{20}= 230 \end{align} \]

# 手計算
(((25 - 55)^2) * 1 + ((35 - 55)^2) * 3 + ((45 - 55)^2) * 3 + ((55 - 55)^2) * 
    5 + ((65 - 55)^2) * 5 + ((75 - 55)^2) * 2 + ((85 - 55)^2) * 1)/20

[1] 230

# 合計を算出するsum関数を使う
代表値 <- c(25, 35, 45, 55, 65, 75, 85)
Bクラスの度数 <- c(1, 3, 3, 5, 5, 2, 1)
Bクラスの人数 <- 20
Bクラスの平均 <- 55

sum(((代表値 - Bクラスの平均)^2) * Bクラスの度数)/Bクラスの人数

[1] 230

• クラスBの標準偏差

\[ \begin{align} s=\sqrt{230}\risingdotseq 15.166 \end{align} \]

print(sqrt(230), digits = 5)

[1] 15.166

例題の回答まとめ

この結果、両クラスの平均点は等しいが、Bクラスの方が標準偏差が大きいので、BクラスはAクラスよりもデータの散らばりの度合いが大きいと言える。