ベイズ推定の概要

超入門

@広島ベイズ塾

Created by Yoshitake TAKEBAYASHI / @psycle44

自己紹介

名前:　竹林由武

所属:　統計数理研究所

専門:　疫学、臨床心理学


研究テーマ：

　自殺の時空間疫学
　小研究数メタ分析
　ウェルビーイング向上による精神疾患予防
　猫の気持ち

自殺の時空間疫学

http://ikiru.ncnp.go.jp/ikiru-hp/genjo/toukei/index.html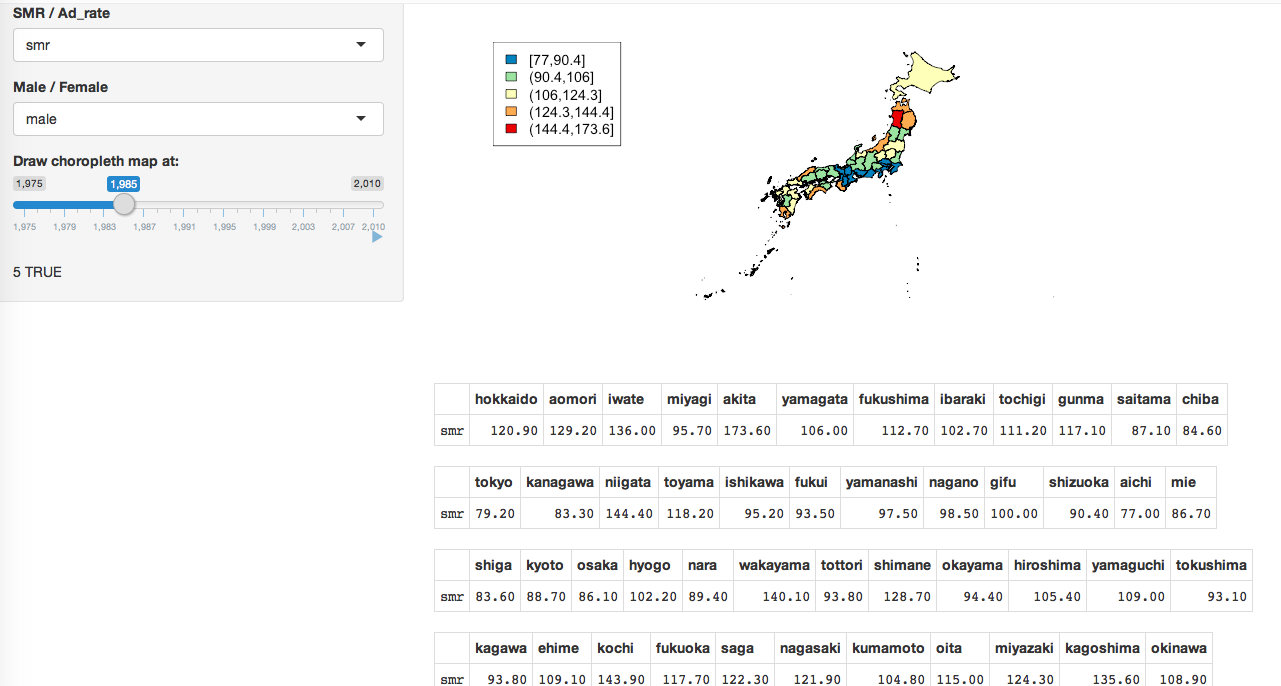

少研究数のメタ分析

Noma, H. Statist. Med. 2011, 30 3304–3312

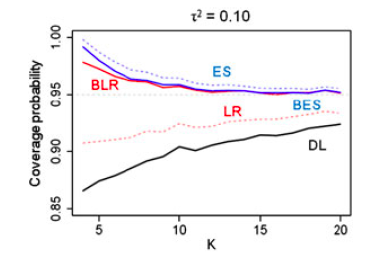
K=10以下での信頼区間を向上させる

Topics

  • はじめに

  • 推測統計の基本

  • 最尤推定とベイズ推定

  • MCMCによるベイズ推定






21世紀のマイクロソフト社の基本戦略は

ベイズテクノロジーである

21世紀におけるベイズの発展

21世紀におけるベイズの発展

21世紀におけるベイズの発展

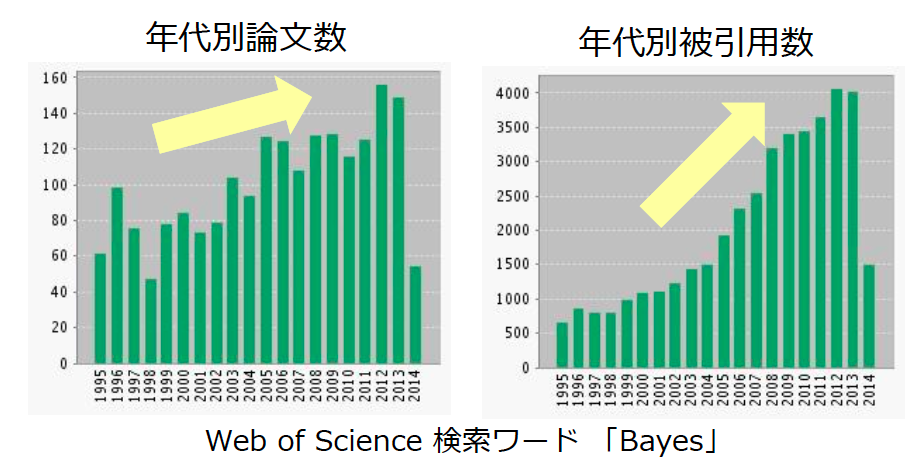
なぜ21世紀？？

ベイズ推定では

膨大な反復計算が必要

PCの処理性能の向上でベイズ推定が実用的に!!

ベイズ推定のメリット

複雑なモデルを推定可能

少サンプル数でも推定可能

従来型の推定法も表現可能

要するに

めっちゃ便利!!

使えると解析の幅が広がる

ベイズ推定を始める前に....

推測統計学のおさらい

ある地域での模試の得点の分布

plot of chunk unnamed-chunk-1

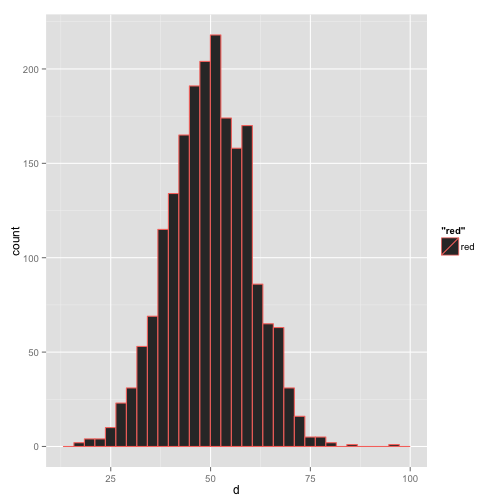
関心:日本全体での分布が知りたい

日本全体での模試得点の分布

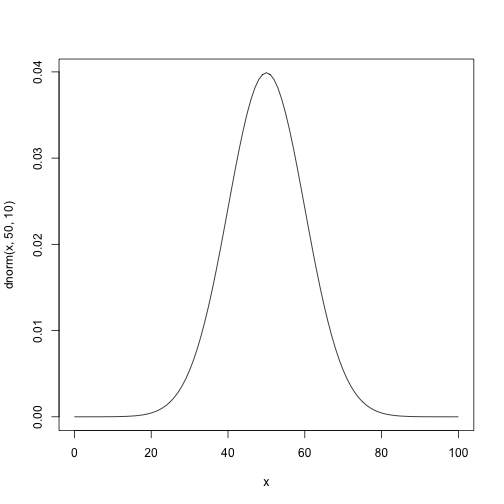
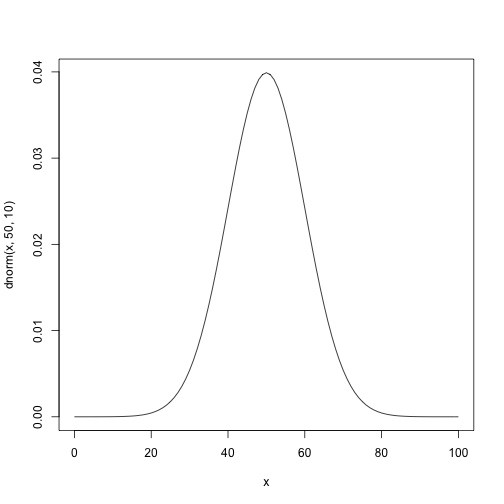
統計モデル:正規分布

$$N(θ,σ^2)$$


$$\ f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-θ)^2}{2\sigma^2}} $$
平均(θ)と分散(σ^2)
で分布の型が決まる

plot of chunk unnamed-chunk-2

統計的推測

得られたデータ
　　(D)
統計モデル
\begin{equation} f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-θ)^2}{2\sigma^2}} \end{equation}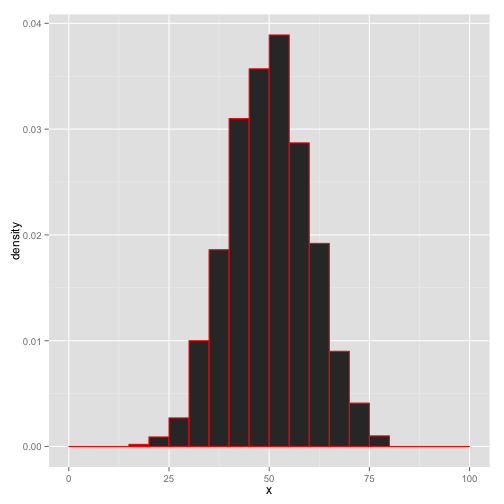
plot of chunk unnamed-chunk-3
plot of chunk unnamed-chunk-4
plot of chunk unnamed-chunk-5
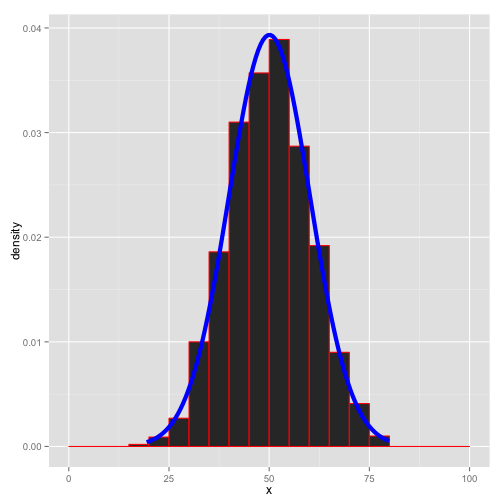
データに最もフィットする
統計モデルのパラメータを探す

データの分布型は多様

データにフィットする分布設定が

統計モデリングの要

様々な分布を知るために

https://ksmzn.shinyapps.io/statdist/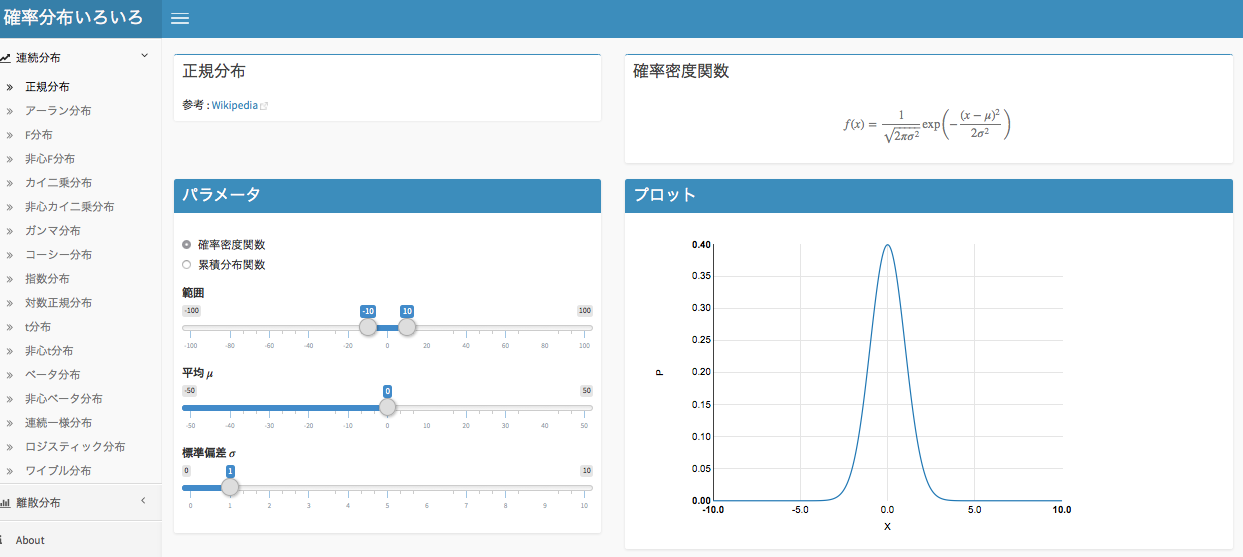

最尤推定とベイズ推定

どちらもパラメータ推定法だけど...

最尤推定法の発想

P(D|θ)が最大になるθを推定する
P(D|θ)=ある母数(θ)の下でデータ(D)が得られる確率

ベイズ推定法の発想

P(θ|D)を推定する
P(θ|D)=あるデータ(D)の下で母数(θ)が得られる確率

最尤推定法の発想

P(D|θ)が最大になるθを推定する

最尤推定法の発想

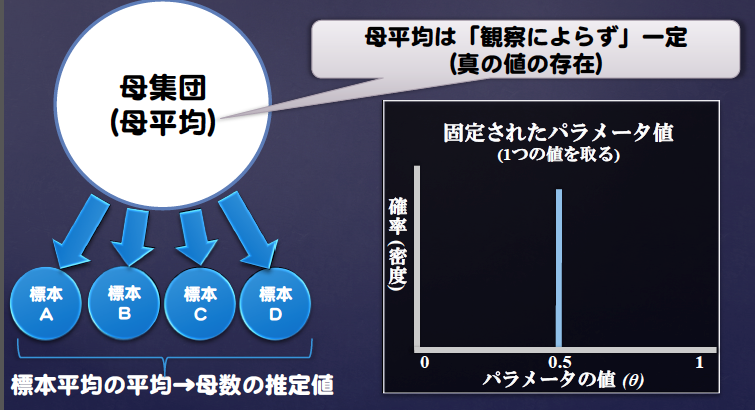
信頼区間の意味

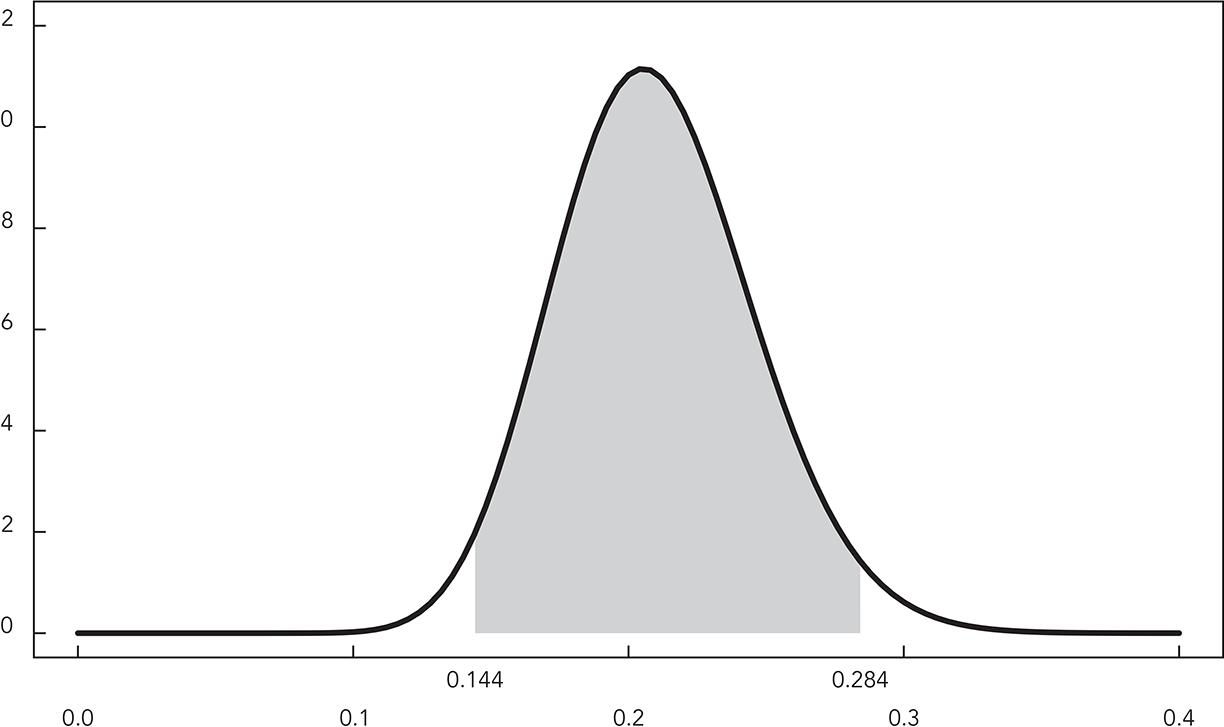
何度も観測を繰り返せば
95%の確率で真値がこの範囲に入る

真値は一定で観測が確率的に変動する

ベイズ法の発想

P(θ|D)を推定する

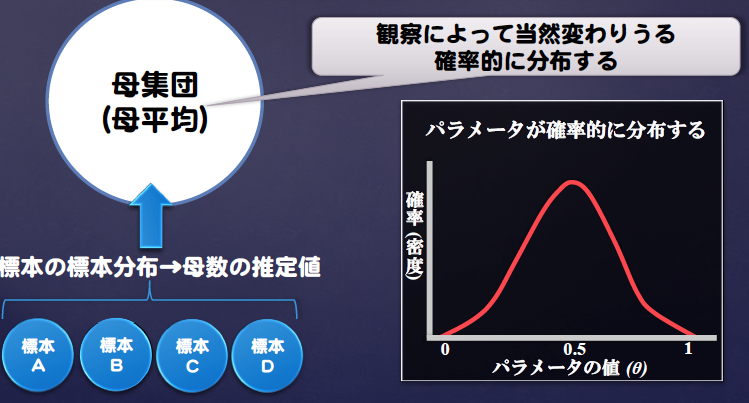
ベイズ法の発想

信用区間の意味

仮に真の値を仮定するなら
真値は95%の確率でこの範囲に入る

$$P(θ|D)$$

はどう求めるのか？


ここに


ベイズの定理あり









ベイズの定理

ベイズの定理

　

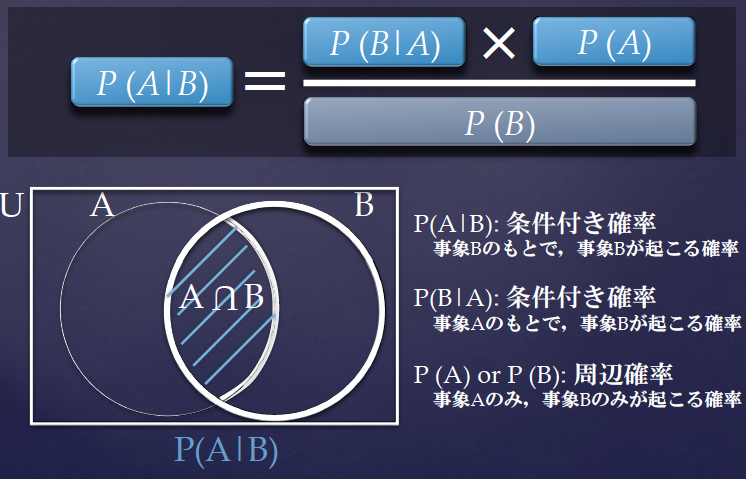
ベイズの定理

パラメータ推定に応用

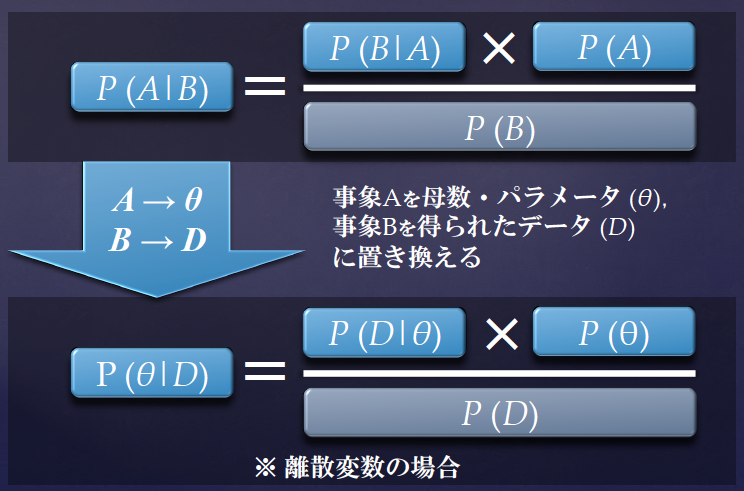
ベイズの定理

パラメータ推定に応用

ベイズの定理

パラメータ推定に応用

ベイズの定理

パラメータ推定に応用

ベイズの定理

パラメータ推定に応用

ベイズの定理

パラメータ推定に応用

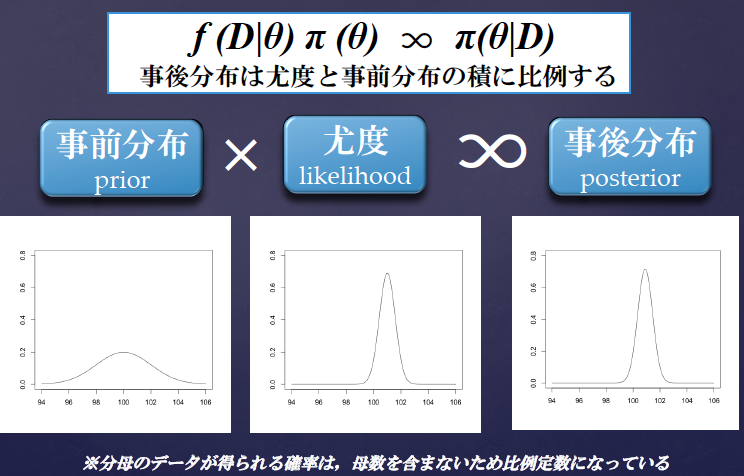
事前分布..???

データに依存せずにθが起こる確率..???

事前分布


  • データ取得前のθの分布に関する情報

  • 研究者の仮説、先行研究、主観

  • データから決める方法もある(客観ベイズ)

事前情報がない場合

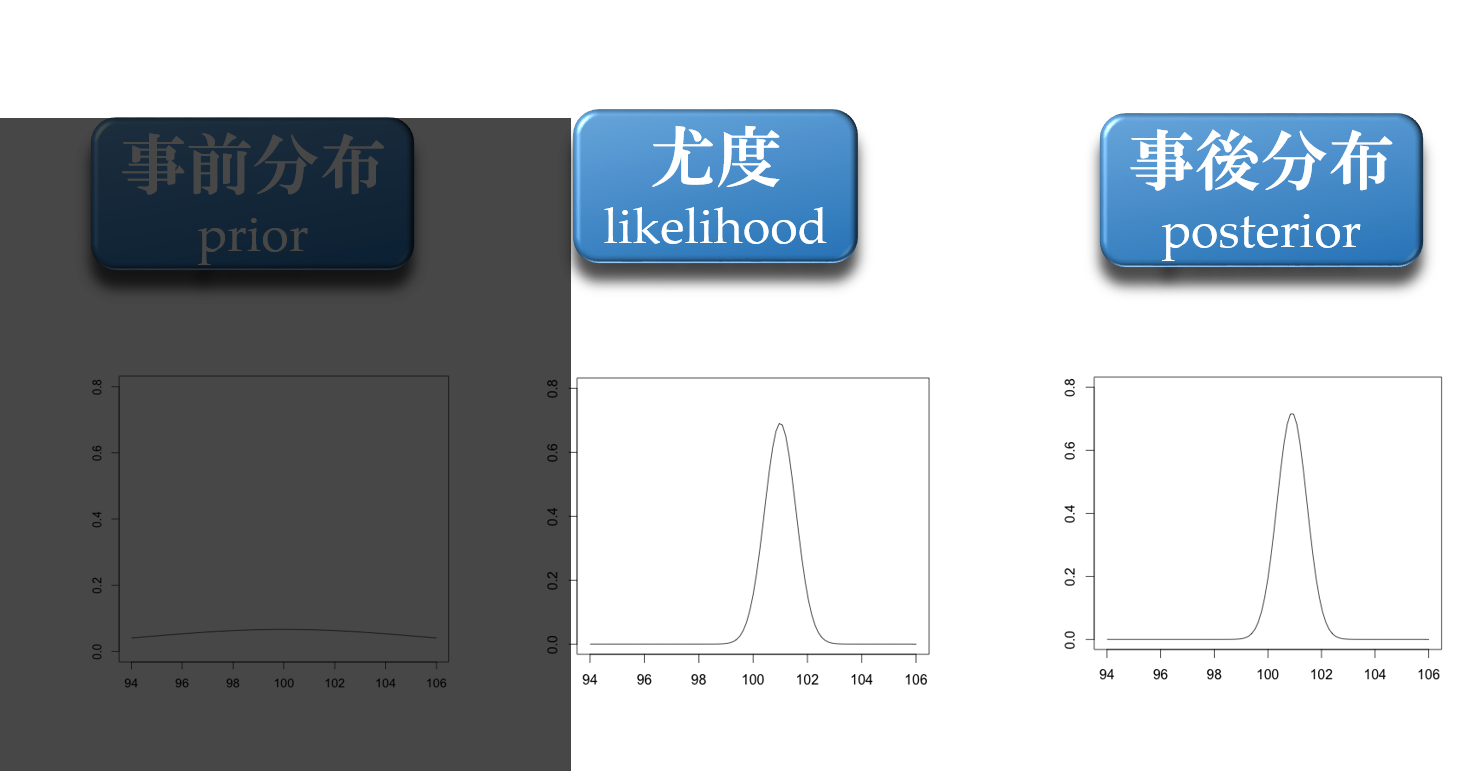
パラメータ推定に
尤度のみ使用

最尤推定と同様の推定結果になる

※推定するパラメータは分布する

ベイズ推定の特徴

パラメータの分布を推定

尤度に加えて事前分布を推定に使用する

要はこれだけ

MCMCによる
ベイズ推定

MCMC

MarcovChainMonteCarlo Methods

マルコフ連鎖モンテカルロ法

マルコフ連鎖モンテカルロ法


移動の方向が一つ前の状態に基づいて決まるルールを付与した 乱数シミュレーションによってパラメータの分布を生成する方法

なぜベイズ推定にMCMC??


  • パラメータの分布を得るのに適してる

  • 解析的に解けないパラメータの分布を
    近似的に求められる

MCMCの代表

メトロポリスヘイスティング法

ギブスサンプリングもその一種

ギブスサンプリング


step1: x1の初期値を指定する

step2: x2を初期値で固定し, x1をサンプリング

step3: x1をstep2の値に固定し, x2をサンプリング

step4: x2をstep3の値に固定して, x1をサンプリング

以下、 step3,4を繰り返す。

なるほどよくわからん

アニメーションで見てみましょう

片方のパラメータで見ると...

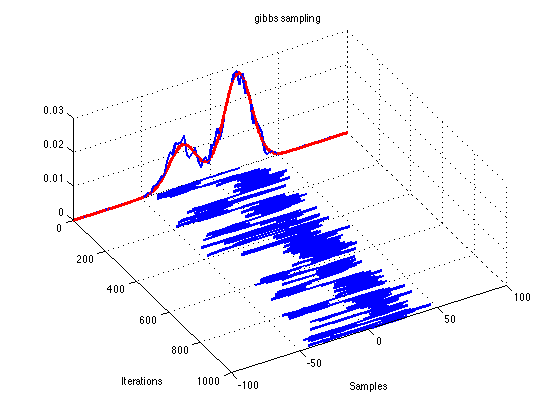
MCMCによるサンプリングが適切であれば
定常分布に収束する

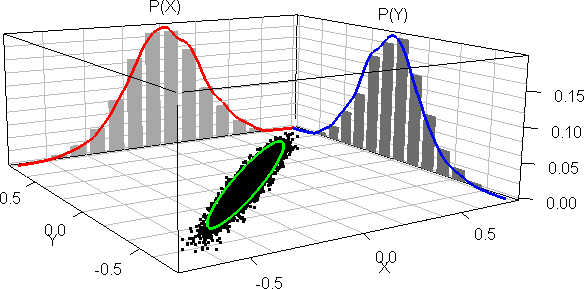
定常分布: 初期値を変えても必ず同一の分布に達する

Burnin区間 Warm-up期間

サンプリング初期は不安定なので推定に使わない

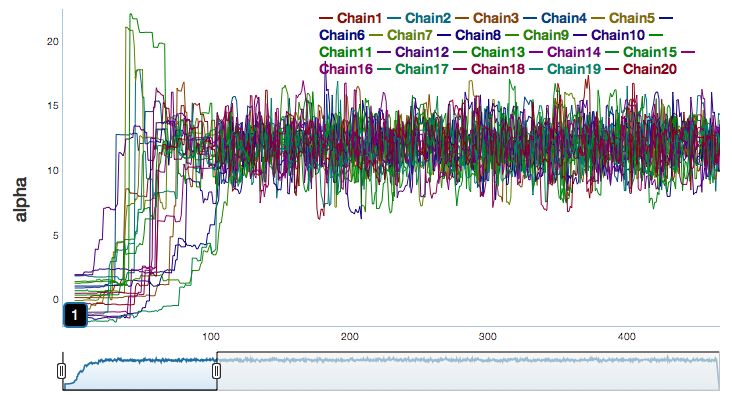
stanはデフォルトで半分捨てる

収束の診断指標

  • Gelman & Rubinの指標

  • Gewekeの指標

  • 自己相関

    •

Gelman & Rubinの指標

plot of chunk unnamed-chunk-6

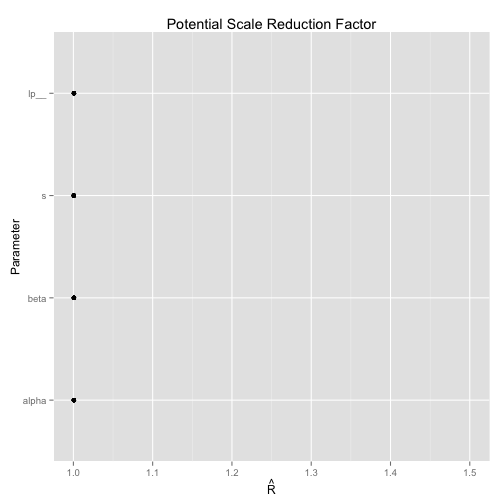
1.01を越えなければ良い

chain間の分散がchain内の分散より小さいと1に近づく

chain間の差を検討

Gewekeの指標

plot of chunk unnamed-chunk-7

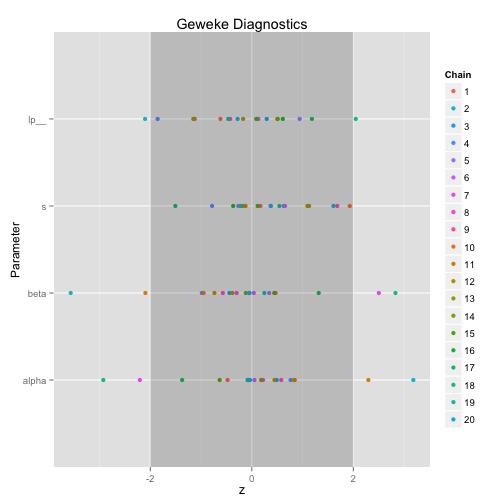
MCMCの最初の方と最後の方の平均に差がないか検定 Z値が±1.96以内に入っていれば差はない→収束してる

自己相関

plot of chunk unnamed-chunk-8

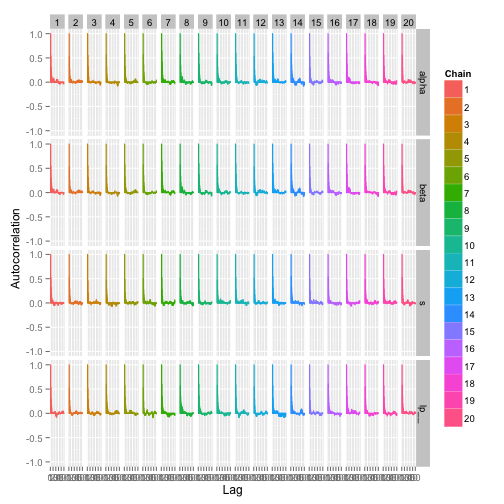
自己相関が5を超えると良くない

MCMCによるベイズ推定

MCMCによる推定の手順

①データを表現する統計モデルの記述
②パラメータの事前分布を設定
③MCMCの実行
④収束診断
⑤事後分布の解釈

回帰モデルの推定

①データを表現する統計モデルの記述


$$f(Y)=α+βX+ε$$


Yは正規分布

$$f(Y)=N(α+βX,ε)$$

②パラメータ事前分布の設定

αとβの分布について情報なし

$$N(0,100)$$
分散が大きい分布を指定

回帰モデルの推定

③MCMCのセッティング

  • 収束回数

  • chainの数

  • burin区間

  • thin(間引き数)

MCMCで回帰モデルの推定

\begin{equation} f(Y)=α+βX+ε \end{equation}

library(rstan)
N <- 500
x <- rnorm(N, mean = 50, sd = 10)
y <- 10 + 0.8 * x + rnorm(N, mean =0, sd = 7)

stancode <- '
  data{ int N; 
        real x[N]; 
        real y[N]; 
        }  
  parameters { real alpha; 
               real beta; 
              real s;
              }
  model{ for(i in 1:N) 
          y[i] ~ normal(alpha + beta * x[i], s); #推定するモデル
          alpha ~ normal(0, 100); #パラメータの事前分布
          beta ~ normal(0, 100);  #パラメータの事前分布
          s ~ inv_gamma(0.001, 0.001);
          }
'

世界で二番目に簡単なStanコード

 

datastan <- list(N=N, x=x, y=y)
fit <- stan(model_code = stancode,data=datastan,iter=5000,chain=4)

my_shinystan <- as.shinystan(fit)
launch_shinystan(my_shinystan)

推定結果を見てみよう
On the shinyRStan

shinyStanの例

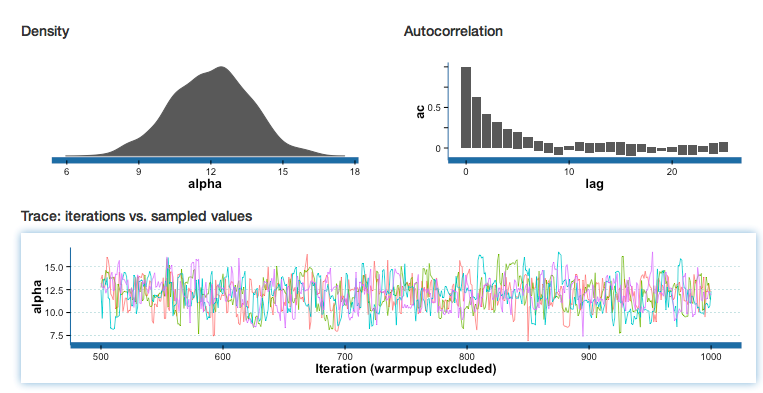
事後分布・自己相関

トレースプロット

事後分布の要約統計

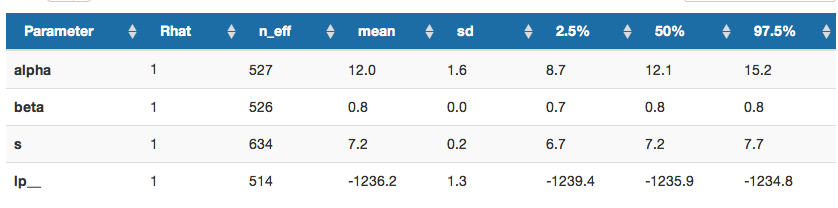
平均・標準偏差・信用区間

論文ではこんな風に報告

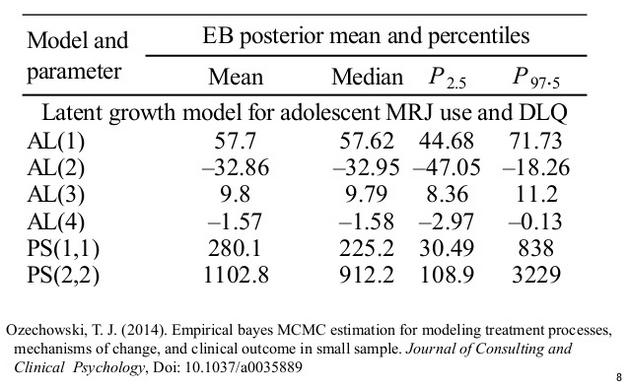
ベイズ推定の報告の仕方

ベイズ推定が活きる

研究例

小症例数でのSEM

マルチレベル因子分析

まとめ

  • ベイズ推定はパラメータの分布を推定
  • ベイズ推定は事前分布を利用する
  • ベイズ推定はMCMCで行う
  • Rhat等の指標で収束判断
  • 複雑なモデルもMCMCがあれば怖くない

Enjoy!!